Skip to contents

Sample the hierarchical stochastic block model

Source: R/games.R
sample_hierarchical_sbm.Rd

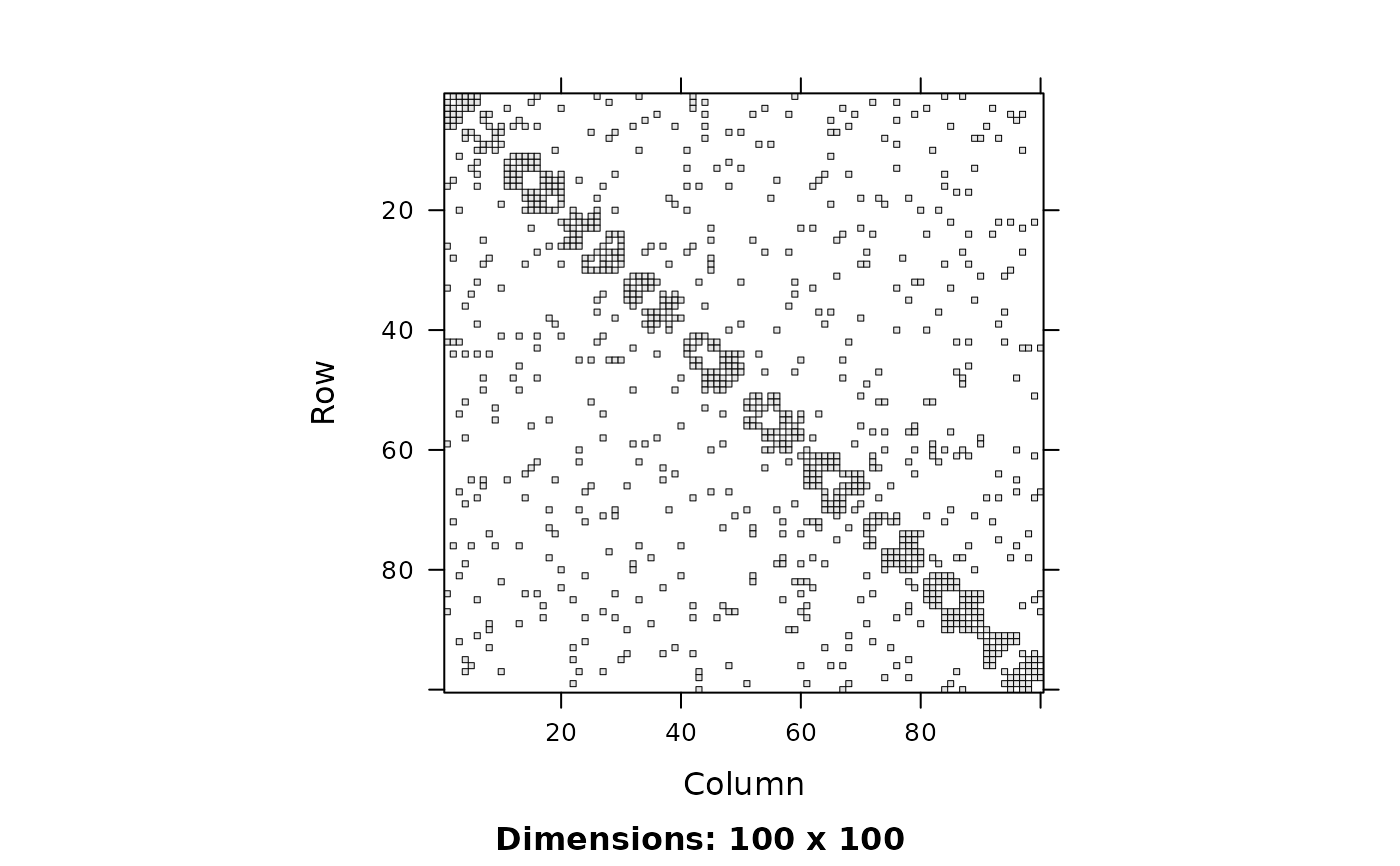
Sampling from a hierarchical stochastic block model of networks.

Usage

sample_hierarchical_sbm(n, m, rho, C, p)

hierarchical_sbm(...)

Arguments

n

Integer scalar, the number of vertices.

m

Integer scalar, the number of vertices per block. n / m must be integer. Alternatively, an integer vector of block sizes, if not all the blocks have equal sizes.

rho

Numeric vector, the fraction of vertices per cluster, within a block. Must sum up to 1, and rho * m must be integer for all elements of rho. Alternatively a list of rho vectors, one for each block, if they are not the same for all blocks.

C

A square, symmetric numeric matrix, the Bernoulli rates for the clusters within a block. Its size must mach the size of the rho vector. Alternatively, a list of square matrices, if the Bernoulli rates differ in different blocks.

p

Numeric scalar, the Bernoulli rate of connections between vertices in different blocks.

...

Passed to sample_hierarchical_sbm().

Value

An igraph graph.

Details

The function generates a random graph according to the hierarchical stochastic block model.

See also

Random graph models (games) bipartite_gnm(), erdos.renyi.game(), sample_(), sample_bipartite(), sample_chung_lu(), sample_correlated_gnp(), sample_correlated_gnp_pair(), sample_degseq(), sample_dot_product(), sample_fitness(), sample_fitness_pl(), sample_forestfire(), sample_gnm(), sample_gnp(), sample_grg(), sample_growing(), sample_islands(), sample_k_regular(), sample_last_cit(), sample_pa(), sample_pa_age(), sample_pref(), sample_sbm(), sample_smallworld(), sample_traits_callaway(), sample_tree()

Author

Gabor Csardi csardi.gabor@gmail.com

hsbm_game(), hsbm_list_game().

Examples


## Ten blocks with three clusters each
C <- matrix(c(
  1, 3 / 4, 0,
  3 / 4, 0, 3 / 4,
  0, 3 / 4, 3 / 4
), nrow = 3)
g <- sample_hierarchical_sbm(100, 10, rho = c(3, 3, 4) / 10, C = C, p = 1 / 20)
g
#> IGRAPH c355119 U--- 100 444 -- Hierarchical stochastic block model
#> + attr: name (g/c), m (g/n), rho (g/n), C (g/n), p (g/n)
#> + edges from c355119:
#>  [1]  1-- 2  1-- 3  2-- 3  1-- 4  2-- 4  3-- 4  2-- 5  1-- 6  5-- 7  4-- 8
#> [11]  5-- 8  6-- 8  4-- 9  6-- 9  4--10  6--10  8-- 9  7--10  8--10  9--10
#> [21] 11--12 11--13 12--13 11--14 13--14 11--15 12--15 13--15 11--16 12--16
#> [31] 13--16 14--17 15--17 14--18 16--18 14--19 15--19 16--19 14--20 15--20
#> [41] 16--20 17--18 17--19 18--19 17--20 18--20 19--20 21--22 21--23 22--23
#> [51] 22--24 23--24 21--25 22--25 23--25 21--26 23--26 24--27 26--27 24--28
#> [61] 25--28 24--29 25--29 26--29 24--30 25--30 26--30 27--28 27--29 28--29
#> [71] 27--30 28--30 29--30 31--32 31--33 32--33 31--34 32--34 33--34 31--35
#> + ... omitted several edges

library("Matrix")
image(g[])