SIR model on graphs

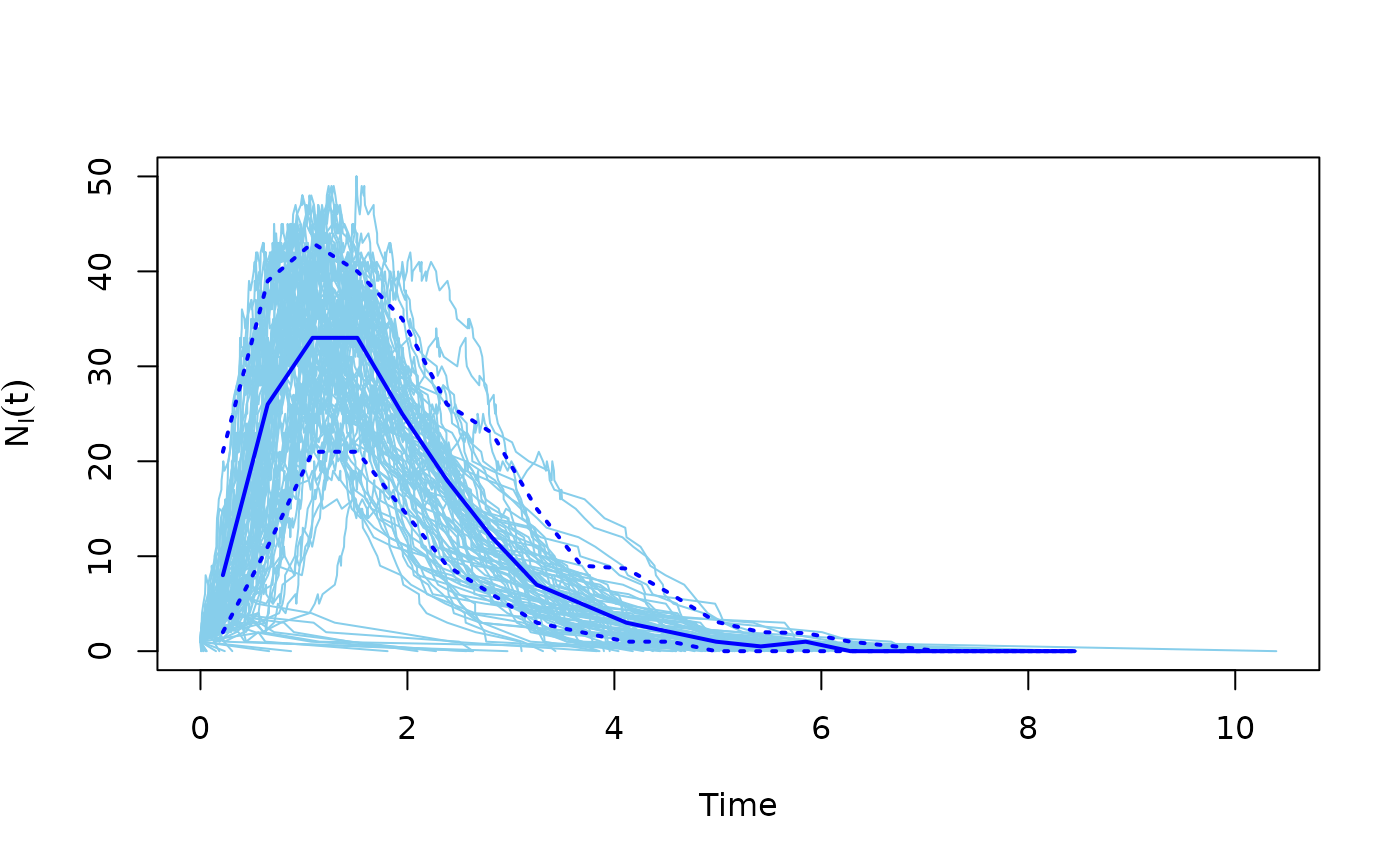
Run simulations for an SIR (susceptible-infected-recovered) model, on a graph

Usage

time_bins(x, middle = TRUE)

# S3 method for class 'sir'
time_bins(x, middle = TRUE)

# S3 method for class 'sir'
median(x, na.rm = FALSE, ...)

# S3 method for class 'sir'
quantile(x, comp = c("NI", "NS", "NR"), prob, ...)

sir(graph, beta, gamma, no.sim = 100)

Arguments

x: A sir object, returned by the sir() function.
middle: Logical scalar, whether to return the middle of the time bins, or the boundaries.
na.rm: Logical scalar, whether to ignore NA values. sir objects do not contain any NA values currently, so this argument is effectively ignored.
...: Additional arguments, ignored currently.
comp: Character scalar. The component to calculate the quantile of. NI is infected agents, NS is susceptibles, NR stands for recovered.
prob: Numeric vector of probabilities, in [0,1], they specify the quantiles to calculate.
graph: The graph to run the model on. If directed, then edge directions are ignored and a warning is given.
beta: Non-negative scalar. The rate of infection of an individual that is susceptible and has a single infected neighbor. The infection rate of a susceptible individual with n infected neighbors is n times beta. Formally this is the rate parameter of an exponential distribution.
gamma: Positive scalar. The rate of recovery of an infected individual. Formally, this is the rate parameter of an exponential distribution.
no.sim: Integer scalar, the number simulation runs to perform.

Value

For sir() the results are returned in an object of class ‘sir’, which is a list, with one element for each simulation. Each simulation is itself a list with the following elements. They are all numeric vectors, with equal length:

times: The times of the events.
NS: The number of susceptibles in the population, over time.
NI: The number of infected individuals in the population, over time.
NR: The number of recovered individuals in the population, over time.

Function time_bins() returns a numeric vector, the middle or the boundaries of the time bins, depending on the middle argument.

median returns a list of three named numeric vectors, NS, NI and NR. The names within the vectors are created from the time bins.

quantile returns the same vector as median (but only one, the one requested) if only one quantile is requested. If multiple quantiles are requested, then a list of these vectors is returned, one for each quantile.

Details

The SIR model is a simple model from epidemiology. The individuals of the population might be in three states: susceptible, infected and recovered. Recovered people are assumed to be immune to the disease. Susceptibles become infected with a rate that depends on their number of infected neighbors. Infected people become recovered with a constant rate.

The function sir() simulates the model. This function runs multiple simulations, all starting with a single uniformly randomly chosen infected individual. A simulation is stopped when no infected individuals are left.

Function time_bins() bins the simulation steps, using the Freedman-Diaconis heuristics to determine the bin width.

Function median and quantile calculate the median and quantiles of the results, respectively, in bins calculated with time_bins().

References

Bailey, Norman T. J. (1975). The mathematical theory of infectious diseases and its applications (2nd ed.). London: Griffin.

Author

Gabor Csardi csardi.gabor@gmail.com. Eric Kolaczyk (http://math.bu.edu/people/kolaczyk/) wrote the initial version in R.

igraph_sir().

Examples


g <- sample_gnm(100, 100)
sm <- sir(g, beta = 5, gamma = 1)
plot(sm)